理论
在大语言模型的强化学习训练中,有reward shaping和KL loss两种引入KL散度约束的方式,前者为直接对reward值加上kl估计,作为一个新的reward $r \leftarrow r - \beta\cdot KL$;另外一种为将KL估计量放到loss中,计算 $\nabla_\theta \operatorname{KL}(\pi_\theta||\pi_{ref})$,一起进行反向传播.
Schulman (2020) 给出了三种KL散度的估计方式,其中k3 loss被认为是兼备unbiased和low variance的好估计量。,DeepSeek的GRPO算法 (Guo et al. 2025) 就使用了这种方式:
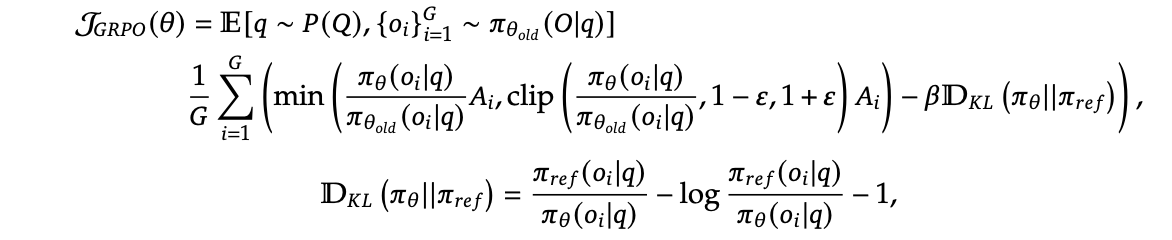
Fig. 1. GRPO 算法. (来源:Guo et al. 2025)
不过,如果使用KL Loss,我们实际上是通过抽样来对KL散度的梯度做估计,这和Schulman (2020) 的分析有一些区别。在训练中,我们构建了估计量后,将其直接作为loss进行反向传播求导,期望这仍然是一个很好的逼近:
$$ \begin{align*} \nabla_\theta \widehat{\operatorname{KL}}(X) &\approx \nabla_\theta \operatorname{KL}(\pi_\theta||\pi_{\theta_{ref}})=\nabla_\theta \int \pi_\theta(x)\cdot\log\left(\frac{\pi_\theta(x)}{\pi_{ref}(x)}\right)dx\\ &= \int \nabla_\theta\pi_\theta(x)\cdot\log\left(\frac{\pi_\theta(x)}{\pi_{ref}(x)}\right) + \pi_\theta(x)\nabla_\theta\log\pi_\theta(x)dx\\ &=\int \pi_\theta(x)\cdot\nabla_\theta\log\pi_\theta(x)\log\left(\frac{\pi_\theta(x)}{\pi_{ref}(x)}\right) + \pi_\theta(x)\cdot \frac{1}{\pi_\theta(x)}\nabla_\theta\pi_\theta(x)dx\\ &=E_{x\sim\pi_\theta}\left[\nabla_\theta\log\pi_\theta(X)\cdot\log\left(\frac{\pi_\theta(X)}{\pi_{ref}(X)}\right)\right]. \end{align*} $$
但KL的无偏估计的梯度,未必是KL的梯度的无偏估计,
$$ E_{\pi_\theta}[\nabla_\theta \widehat{\operatorname{KL}}(X)] \neq \nabla_\theta E_{\pi_\theta}[ \widehat{\operatorname{KL}}(X)] = \nabla_\theta \operatorname{KL}(\pi_\theta||\pi_{\theta_{ref}}). $$
事实上,他们之间差了一项:
$$ \begin{align*} \nabla_\theta E_{\pi_\theta}[f_\theta(X)] &= \int \nabla_\theta\pi_\theta(x)\cdot f_\theta(x) + \pi_\theta(x)\cdot\nabla_\theta f_\theta(x) dx\\ &= \int \pi_\theta(x)\cdot\nabla_\theta \log\pi_\theta(x)\cdot f_\theta(x) dx + \int \pi_\theta(x)\cdot\nabla_\theta f_\theta(x) dx\\ &= E_{\pi_\theta}[\nabla_\theta\log\pi_\theta(X)\cdot f_\theta(X)] + E_{\pi_\theta}[\nabla_\theta f_\theta(X)]. \end{align*} $$
对于policy生成的样本 $X\sim\pi_\theta(\cdot)$,分别取 $\widehat{\operatorname{KL}}$ 为k1、k2、k3 loss可知,
-
k1
$$ \begin{align*} \widehat{\operatorname{KL}}(X) &= \log\pi_\theta(X) - \log\pi_{ref}(X);\\ \nabla_\theta \widehat{\operatorname{KL}}(X) &= \nabla_\theta\log\pi_\theta(X);\\ E_{\pi_\theta}[\nabla_\theta \widehat{\operatorname{KL}}(X)] &= \int \pi_\theta(x)\cdot \frac{1}{\pi_\theta(x)}\nabla_\theta\pi_\theta(x)dx=0 \neq \nabla_\theta \operatorname{KL}(\pi_\theta||\pi_{\theta_{ref}}). \end{align*} $$
-
k2
$$ \begin{align*} \widehat{\operatorname{KL}}(X) &= \frac{1}{2}(\log\pi_\theta(X) - \log\pi_{ref}(X))^2;\\ \nabla_\theta \widehat{\operatorname{KL}}(X) &= \nabla_\theta\log\pi_\theta(X)\cdot\log\left(\frac{\pi_\theta(X)}{\pi_{ref}(X)}\right);\\ E_{\pi_\theta}[\nabla_\theta \widehat{\operatorname{KL}}(X)] &= E_{\pi_\theta}\left[\nabla_\theta\log\pi_\theta(X) \cdot \log\left(\frac{\pi_\theta(X)}{\pi_{ref}(X)}\right)\right] = \nabla_\theta \operatorname{KL}(\pi_\theta||\pi_{\theta_{ref}}). \end{align*} $$
-
k3
$$ \begin{align*} \widehat{\operatorname{KL}}(X) &= \frac{\pi_{ref}(X)}{\pi_\theta(X)} - 1 - \log\left(\frac{\pi_{ref}(X)}{\pi_\theta(X)}\right);\\ \nabla_\theta \widehat{\operatorname{KL}}(X) &= \nabla_\theta\log\pi_\theta(X) \cdot \left(1 - \frac{\pi_{ref}(X)}{\pi_\theta(X)}\right);\\ E_{\pi_\theta}[\nabla_\theta \widehat{\operatorname{KL}}(X)] &= E_{\pi_\theta}\left[\nabla_\theta\log\pi_\theta(X) \cdot \left(1 - \frac{\pi_{ref}(X)}{\pi_\theta(X)}\right)\right]\neq \nabla_\theta \operatorname{KL}(\pi_\theta||\pi_{\theta_{ref}}). \end{align*} $$
可见,虽然k2 loss并不是kl的无偏估计,但其梯度是kl的梯度的无偏估计;而k1和k3则相反。值得注意的是,k1 loss的梯度的期望始终为0,在大的batch size条件下,这是平凡的。这也说明了GRPO算法中采用的KL loss不是一个很好的估计量。
有时大家还会使用逆KL散度,它将policy model和reference model在KL散度的计算中交换位置。由于样本 $X$ 始终是从policy model中抽出,我们需要乘以一个probability ratio,
$$ \begin{align*} \operatorname{KL}(\pi_{ref}||\pi_\theta) &= E_{X\sim\pi_{ref}}\left[ \log\left(\frac{\pi_{ref}(X)}{\pi_\theta(X)}\right) \right] = E_{X\sim\pi_{\theta}}\left[ \frac{\pi_{ref}(X)}{\pi_\theta(X)} \cdot \log\left(\frac{\pi_{ref}(X)}{\pi_\theta(X)}\right) \right]; \\ \nabla_\theta \operatorname{KL}(\pi_{ref}||\pi_\theta) &= E_{X\sim\pi_{ref}} [-\nabla_\theta \log \pi_\theta(X)] = E_{X\sim\pi_{\theta}}\left[ - \frac{\pi_{ref}(X)}{\pi_\theta(X)} \cdot \nabla_\theta \log \pi_\theta(X) \right] \\ &= E_{X\sim\pi_{\theta}}\left[ \left(- \frac{\pi_{ref}(X) }{\pi_\theta(X)^2} \right) \cdot \nabla_\theta \pi_\theta(X) \right] \\ &= E_{X\sim\pi_{\theta}}\left[ \nabla_\theta \left(\frac{\pi_{ref}(X) }{\pi_\theta(X)} \right) \right]. \end{align*} $$
于是,如果要在KL loss中估计其梯度,一个无偏估计可取
$$ \widehat{\operatorname{KL}}(X) = \frac{\pi_{ref}(X) }{\pi_\theta(X)}. $$
此时KL的无偏估计的梯度仍然不等于KL的梯度的无偏估计:
$$ \begin{align*} \widehat{\operatorname{KL}}(X) &= \frac{\pi_{ref}(X)}{\pi_\theta(X)} \cdot \log\left(\frac{\pi_{ref}(X)}{\pi_\theta(X)}\right); \\ E_{X\sim\pi_{\theta}}[\nabla_\theta \widehat{\operatorname{KL}}(X)] &= E_{X\sim\pi_{\theta}} \left[ \left(\frac{\pi_{ref}(X)}{\pi_\theta(X)}\right) \cdot (- \nabla_\theta\log\pi_\theta(X)) \cdot \left( 1 + \frac{\pi_{ref}(X)}{\pi_\theta(X)}\right) \right] \\ &= E_{X\sim\pi_{ref}} \left[ (- \nabla_\theta\log\pi_\theta(X)) \cdot \left( 1 + \frac{\pi_{ref}(X)}{\pi_\theta(X)}\right) \right] \\ &\neq E_{X\sim\pi_{ref}} [-\nabla_\theta \log \pi_\theta(X)] = \nabla_\theta \operatorname{KL}(\pi_{ref}||\pi_\theta). \end{align*} $$
实验
考虑 $\pi_\theta=\mathcal{N}(0,1),~\pi_{ref}=\mathcal{N}(1,1.1)$,参数 $\theta$ 为高斯分布的均值和标准差,估计结果与理论分析一致:
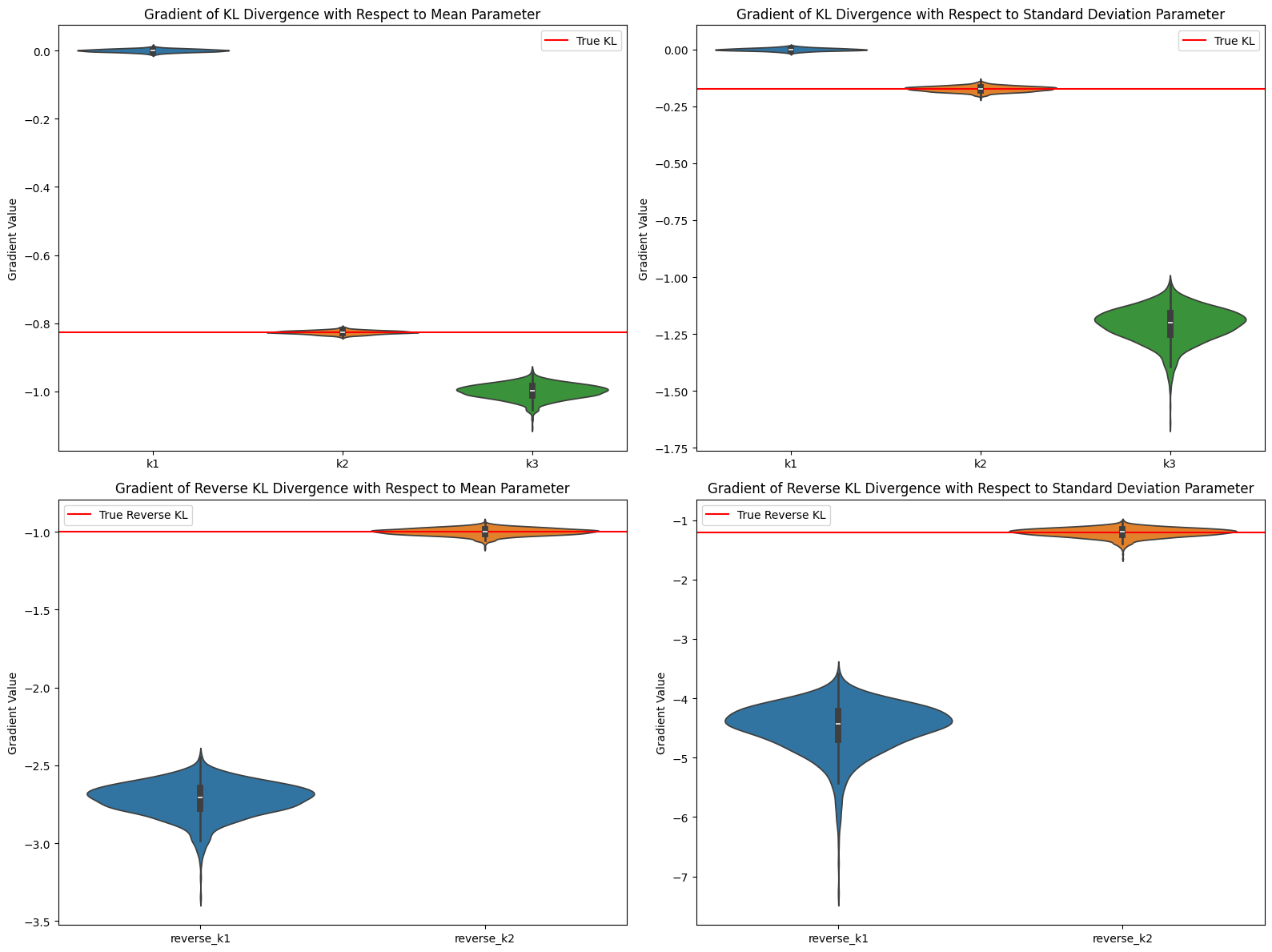
Fig. 2. KL估计实验结果
Average gradient value comparison (mean parameter):
True KL gradient: -0.826446
k1 average gradient: 0.000137
k2 average gradient: -0.826291
k3 average gradient: -0.999618
Average gradient value comparison (standard deviation parameter):
True KL gradient: -0.173554
k1 average gradient: -0.000104
k2 average gradient: -0.173379
k3 average gradient: -1.209091
Reverse KL - Average gradient value comparison (mean parameter):
True Reverse KL gradient: -1.000000
reverse_k1 average gradient: -2.718389
reverse_k2 average gradient: -0.999755
Reverse KL - Average gradient value comparison (standard deviation parameter):
True Reverse KL gradient: -1.210000
reverse_k1 average gradient: -4.496196
reverse_k2 average gradient: -1.208987
KL - Comparison of bias and standard deviation for mean parameter gradients:
╒════╤═════════════╤══════════════╕
│ │ bias/true │ stdev/true │
╞════╪═════════════╪══════════════╡
│ k1 │ 1.0002 │ 0.0054 │
├────┼─────────────┼──────────────┤
│ k2 │ 0.0002 │ 0.0065 │
├────┼─────────────┼──────────────┤
│ k3 │ 0.2095 │ 0.026 │
╘════╧═════════════╧══════════════╛
KL - Comparison of bias and standard deviation for standard deviation parameter gradients:
╒════╤═════════════╤══════════════╕
│ │ bias/true │ stdev/true │
╞════╪═════════════╪══════════════╡
│ k1 │ 0.9994 │ 0.0359 │
├────┼─────────────┼──────────────┤
│ k2 │ 0.001 │ 0.0686 │
├────┼─────────────┼──────────────┤
│ k3 │ 5.9667 │ 0.4311 │
╘════╧═════════════╧══════════════╛
Reverse KL - Comparison of bias and standard deviation for mean parameter gradients:
╒════════════╤═════════════╤══════════════╕
│ │ bias/true │ stdev/true │
╞════════════╪═════════════╪══════════════╡
│ reverse_k1 │ 1.7184 │ 0.1081 │
├────────────┼─────────────┼──────────────┤
│ reverse_k2 │ 0.0002 │ 0.0231 │
╘════════════╧═════════════╧══════════════╛
Reverse KL - Comparison of bias and standard deviation for standard deviation parameter gradients:
╒════════════╤═════════════╤══════════════╕
│ │ bias/true │ stdev/true │
╞════════════╪═════════════╪══════════════╡
│ reverse_k1 │ 2.7159 │ 0.3419 │
├────────────┼─────────────┼──────────────┤
│ reverse_k2 │ 0.0008 │ 0.0636 │
╘════════════╧═════════════╧══════════════╛
实验代码
import torch
import numpy as np
import matplotlib.pyplot as plt
from torch.distributions import Normal
import seaborn as sns
# Set random seed for reproducibility
torch.manual_seed(42)
np.random.seed(42)
# Define parameters for two normal distributions
def setup_distributions(mu_theta=0.0, sigma_theta=1.0, mu_ref=1.0, sigma_ref=1.1):
# Create trainable parameters
mu_theta_param = torch.tensor(mu_theta, requires_grad=True)
sigma_theta_param = torch.tensor(sigma_theta, requires_grad=True)
# Reference distribution parameters (fixed)
mu_ref_param = torch.tensor(mu_ref)
sigma_ref_param = torch.tensor(sigma_ref)
# Create distributions
pi_theta = Normal(mu_theta_param, sigma_theta_param)
pi_ref = Normal(mu_ref_param, sigma_ref_param)
return pi_theta, pi_ref, mu_theta_param, sigma_theta_param
# Calculate the true KL divergence (analytical solution for normal distributions)
def true_kl_divergence(pi_theta, pi_ref):
mu_theta = pi_theta.loc
sigma_theta = pi_theta.scale
mu_ref = pi_ref.loc
sigma_ref = pi_ref.scale
kl = (torch.log(sigma_ref/sigma_theta) +
(sigma_theta**2 + (mu_theta - mu_ref)**2)/(2*sigma_ref**2) - 0.5)
rkl = (torch.log(sigma_theta/sigma_ref) +
(sigma_ref**2 + (mu_ref - mu_theta)**2)/(2*sigma_theta**2) - 0.5)
return kl, rkl
# Three different KL divergence estimates
def k1_loss(x, pi_theta, pi_ref):
return pi_theta.log_prob(x) - pi_ref.log_prob(x)
def k2_loss(x, pi_theta, pi_ref):
return 0.5 * (pi_theta.log_prob(x) - pi_ref.log_prob(x))**2
def k3_loss(x, pi_theta, pi_ref):
ratio = torch.exp(pi_ref.log_prob(x) - pi_theta.log_prob(x))
return ratio - 1 - torch.log(ratio)
# Two different reverse KL divergence estimates
def reverse_k1_loss(x, pi_theta, pi_ref):
ratio = torch.exp(pi_ref.log_prob(x) - pi_theta.log_prob(x))
return ratio * (pi_ref.log_prob(x) - pi_theta.log_prob(x))
def reverse_k2_loss(x, pi_theta, pi_ref):
return torch.exp(pi_ref.log_prob(x) - pi_theta.log_prob(x))
# Sample and compute gradients
def estimate_gradients(sample_size=10000, num_trials=10):
pi_theta, pi_ref, mu_param, sigma_param = setup_distributions()
# Compute the gradient of the true and reverse KL divergence
true_kl, true_reverse_kl = true_kl_divergence(pi_theta, pi_ref)
true_kl.backward()
true_grad_mu = mu_param.grad.item()
true_grad_sigma = sigma_param.grad.item()
mu_param.grad.zero_()
sigma_param.grad.zero_()
true_reverse_kl.backward()
true_reverse_grad_mu = mu_param.grad.item()
true_reverse_grad_sigma = sigma_param.grad.item()
mu_param.grad.zero_()
sigma_param.grad.zero_()
# Store gradients from different estimates
k1_grads_mu = []
k1_grads_sigma = []
k2_grads_mu = []
k2_grads_sigma = []
k3_grads_mu = []
k3_grads_sigma = []
reverse_k1_grads_mu = []
reverse_k1_grads_sigma = []
reverse_k2_grads_mu = []
reverse_k2_grads_sigma = []
for _ in range(num_trials):
pi_theta, pi_ref, mu_param, sigma_param = setup_distributions()
# Sample from the current policy
samples = pi_theta.sample((sample_size,))
# Get gradient of KL estimation
k1_values = k1_loss(samples, pi_theta, pi_ref)
k1_mean = k1_values.mean()
k1_mean.backward()
k1_grads_mu.append(mu_param.grad.item())
k1_grads_sigma.append(sigma_param.grad.item())
mu_param.grad.zero_()
sigma_param.grad.zero_()
k2_values = k2_loss(samples, pi_theta, pi_ref)
k2_mean = k2_values.mean()
k2_mean.backward()
k2_grads_mu.append(mu_param.grad.item())
k2_grads_sigma.append(sigma_param.grad.item())
mu_param.grad.zero_()
sigma_param.grad.zero_()
k3_values = k3_loss(samples, pi_theta, pi_ref)
k3_mean = k3_values.mean()
k3_mean.backward()
k3_grads_mu.append(mu_param.grad.item())
k3_grads_sigma.append(sigma_param.grad.item())
mu_param.grad.zero_()
sigma_param.grad.zero_()
reverse_k1_values = reverse_k1_loss(samples, pi_theta, pi_ref)
reverse_k1_mean = reverse_k1_values.mean()
reverse_k1_mean.backward()
reverse_k1_grads_mu.append(mu_param.grad.item())
reverse_k1_grads_sigma.append(sigma_param.grad.item())
mu_param.grad.zero_()
sigma_param.grad.zero_()
reverse_k2_values = reverse_k2_loss(samples, pi_theta, pi_ref)
reverse_k2_mean = reverse_k2_values.mean()
reverse_k2_mean.backward()
reverse_k2_grads_mu.append(mu_param.grad.item())
reverse_k2_grads_sigma.append(sigma_param.grad.item())
mu_param.grad.zero_()
sigma_param.grad.zero_()
return {
'true_grad_mu': true_grad_mu,
'true_grad_sigma': true_grad_sigma,
'k1_grads_mu': k1_grads_mu,
'k1_grads_sigma': k1_grads_sigma,
'k2_grads_mu': k2_grads_mu,
'k2_grads_sigma': k2_grads_sigma,
'k3_grads_mu': k3_grads_mu,
'k3_grads_sigma': k3_grads_sigma,
'true_reverse_grad_mu': true_reverse_grad_mu,
'true_reverse_grad_sigma': true_reverse_grad_sigma,
'reverse_k1_grads_mu': reverse_k1_grads_mu,
'reverse_k1_grads_sigma': reverse_k1_grads_sigma,
'reverse_k2_grads_mu': reverse_k2_grads_mu,
'reverse_k2_grads_sigma': reverse_k2_grads_sigma
}
def create_nice_table(results):
true_grad_mu = results['true_grad_mu']
true_grad_sigma = results['true_grad_sigma']
true_reverse_grad_mu = results['true_reverse_grad_mu']
true_reverse_grad_sigma = results['true_reverse_grad_sigma']
k1_bias_mu = abs(np.mean(results['k1_grads_mu']) - true_grad_mu) / abs(true_grad_mu)
k2_bias_mu = abs(np.mean(results['k2_grads_mu']) - true_grad_mu) / abs(true_grad_mu)
k3_bias_mu = abs(np.mean(results['k3_grads_mu']) - true_grad_mu) / abs(true_grad_mu)
k1_std_mu = np.std(results['k1_grads_mu']) / abs(true_grad_mu)
k2_std_mu = np.std(results['k2_grads_mu']) / abs(true_grad_mu)
k3_std_mu = np.std(results['k3_grads_mu']) / abs(true_grad_mu)
k1_bias_sigma = abs(np.mean(results['k1_grads_sigma']) - true_grad_sigma) / abs(true_grad_sigma)
k2_bias_sigma = abs(np.mean(results['k2_grads_sigma']) - true_grad_sigma) / abs(true_grad_sigma)
k3_bias_sigma = abs(np.mean(results['k3_grads_sigma']) - true_grad_sigma) / abs(true_grad_sigma)
k1_std_sigma = np.std(results['k1_grads_sigma']) / abs(true_grad_sigma)
k2_std_sigma = np.std(results['k2_grads_sigma']) / abs(true_grad_sigma)
k3_std_sigma = np.std(results['k3_grads_sigma']) / abs(true_grad_sigma)
reverse_k1_bias_mu = abs(np.mean(results['reverse_k1_grads_mu']) - true_reverse_grad_mu) / abs(true_reverse_grad_mu)
reverse_k2_bias_mu = abs(np.mean(results['reverse_k2_grads_mu']) - true_reverse_grad_mu) / abs(true_reverse_grad_mu)
reverse_k1_std_mu = np.std(results['reverse_k1_grads_mu']) / abs(true_reverse_grad_mu)
reverse_k2_std_mu = np.std(results['reverse_k2_grads_mu']) / abs(true_reverse_grad_mu)
reverse_k1_bias_sigma = abs(np.mean(results['reverse_k1_grads_sigma']) - true_reverse_grad_sigma) / abs(true_reverse_grad_sigma)
reverse_k2_bias_sigma = abs(np.mean(results['reverse_k2_grads_sigma']) - true_reverse_grad_sigma) / abs(true_reverse_grad_sigma)
reverse_k1_std_sigma = np.std(results['reverse_k1_grads_sigma']) / abs(true_reverse_grad_sigma)
reverse_k2_std_sigma = np.std(results['reverse_k2_grads_sigma']) / abs(true_reverse_grad_sigma)
# Create table
from tabulate import tabulate
import pandas as pd
df_mu = pd.DataFrame({
'bias/true': [k1_bias_mu, k2_bias_mu, k3_bias_mu],
'stdev/true': [k1_std_mu, k2_std_mu, k3_std_mu]
}, index=['k1', 'k2', 'k3'])
df_reverse_mu = pd.DataFrame({
'bias/true': [reverse_k1_bias_mu, reverse_k2_bias_mu],
'stdev/true': [reverse_k1_std_mu, reverse_k2_std_mu]
}, index=['reverse_k1', 'reverse_k2'])
df_sigma = pd.DataFrame({
'bias/true': [k1_bias_sigma, k2_bias_sigma, k3_bias_sigma],
'stdev/true': [k1_std_sigma, k2_std_sigma, k3_std_sigma]
}, index=['k1', 'k2', 'k3'])
df_reverse_sigma = pd.DataFrame({
'bias/true': [reverse_k1_bias_sigma, reverse_k2_bias_sigma],
'stdev/true': [reverse_k1_std_sigma, reverse_k2_std_sigma]
}, index=['reverse_k1', 'reverse_k2'])
# Format values
df_mu = df_mu.round(4)
df_sigma = df_sigma.round(4)
df_reverse_mu = df_reverse_mu.round(4)
df_reverse_sigma = df_reverse_sigma.round(4)
# Print nice table
print("KL - Comparison of bias and standard deviation for mean parameter gradients:")
print(tabulate(df_mu, headers='keys', tablefmt='fancy_grid'))
print("\nKL - Comparison of bias and standard deviation for standard deviation parameter gradients:")
print(tabulate(df_sigma, headers='keys', tablefmt='fancy_grid'))
print("\nReverse KL - Comparison of bias and standard deviation for mean parameter gradients:")
print(tabulate(df_reverse_mu, headers='keys', tablefmt='fancy_grid'))
print("\nReverse KL - Comparison of bias and standard deviation for standard deviation parameter gradients:")
print(tabulate(df_reverse_sigma, headers='keys', tablefmt='fancy_grid'))
return df_mu, df_sigma, df_reverse_mu, df_reverse_sigma
def visualize_results(results):
fig, axes = plt.subplots(2, 2, figsize=(16, 12))
axes[0,0].axhline(y=results['true_grad_mu'], color='r', linestyle='-', label='True KL')
sns.violinplot(data=[results['k1_grads_mu'], results['k2_grads_mu'], results['k3_grads_mu']], ax=axes[0,0])
axes[0,0].set_title('Gradient of KL Divergence with Respect to Mean Parameter')
axes[0,0].set_xticks([0,1,2])
axes[0,0].set_xticklabels(['k1', 'k2', 'k3'])
axes[0,0].set_ylabel('Gradient Value')
axes[0,0].legend()
axes[0,1].axhline(y=results['true_grad_sigma'], color='r', linestyle='-', label='True KL')
sns.violinplot(data=[results['k1_grads_sigma'], results['k2_grads_sigma'], results['k3_grads_sigma']], ax=axes[0,1])
axes[0,1].set_title('Gradient of KL Divergence with Respect to Standard Deviation Parameter')
axes[0,1].set_xticks([0,1,2])
axes[0,1].set_xticklabels(['k1', 'k2', 'k3'])
axes[0,1].set_ylabel('Gradient Value')
axes[0,1].legend()
axes[1,0].axhline(y=results['true_reverse_grad_mu'], color='r', linestyle='-', label='True Reverse KL')
sns.violinplot(data=[results['reverse_k1_grads_mu'], results['reverse_k2_grads_mu']], ax=axes[1,0])
axes[1,0].set_title('Gradient of Reverse KL Divergence with Respect to Mean Parameter')
axes[1,0].set_xticks([0,1])
axes[1,0].set_xticklabels(['reverse_k1', 'reverse_k2'])
axes[1,0].set_ylabel('Gradient Value')
axes[1,0].legend()
axes[1,1].axhline(y=results['true_reverse_grad_sigma'], color='r', linestyle='-', label='True Reverse KL')
sns.violinplot(data=[results['reverse_k1_grads_sigma'], results['reverse_k2_grads_sigma']], ax=axes[1,1])
axes[1,1].set_title('Gradient of Reverse KL Divergence with Respect to Standard Deviation Parameter')
axes[1,1].set_xticks([0,1])
axes[1,1].set_xticklabels(['reverse_k1', 'reverse_k2'])
axes[1,1].set_ylabel('Gradient Value')
axes[1,1].legend()
plt.tight_layout()
plt.show()
# Print mean comparison
print("Average gradient value comparison (mean parameter):")
print(f"True KL gradient: {results['true_grad_mu']:.6f}")
print(f"k1 average gradient: {np.mean(results['k1_grads_mu']):.6f}")
print(f"k2 average gradient: {np.mean(results['k2_grads_mu']):.6f}")
print(f"k3 average gradient: {np.mean(results['k3_grads_mu']):.6f}")
print("\nAverage gradient value comparison (standard deviation parameter):")
print(f"True KL gradient: {results['true_grad_sigma']:.6f}")
print(f"k1 average gradient: {np.mean(results['k1_grads_sigma']):.6f}")
print(f"k2 average gradient: {np.mean(results['k2_grads_sigma']):.6f}")
print(f"k3 average gradient: {np.mean(results['k3_grads_sigma']):.6f}")
print("\nReverse KL - Average gradient value comparison (mean parameter):")
print(f"True Reverse KL gradient: {results['true_reverse_grad_mu']:.6f}")
print(f"reverse_k1 average gradient: {np.mean(results['reverse_k1_grads_mu']):.6f}")
print(f"reverse_k2 average gradient: {np.mean(results['reverse_k2_grads_mu']):.6f}")
print("\nReverse KL - Average gradient value comparison (standard deviation parameter):")
print(f"True Reverse KL gradient: {results['true_reverse_grad_sigma']:.6f}")
print(f"reverse_k1 average gradient: {np.mean(results['reverse_k1_grads_sigma']):.6f}")
print(f"reverse_k2 average gradient: {np.mean(results['reverse_k2_grads_sigma']):.6f}")
# Add nice table output
print()
df = create_nice_table(results)
if __name__ == "__main__":
sample_size = 50000
num_trials = 1000
results = estimate_gradients(sample_size, num_trials)
visualize_results(results)
补充
k2 loss方差减小的思路,可以模仿 Schulman (2020) 的分析,代入一个零均值统计量,待定系数法求解。
首先对 $\theta$ 逐分量求解,
$$ \begin{align*} \lambda_i^* &= \argmin_\lambda E_{X\sim\pi_\theta}\left[(\nabla_{\theta_i}\log\pi_{\theta}(X))^2 \cdot \left(\log\left(\frac{\pi_\theta(X)}{\pi_{ref}(X)}\right) - \lambda\right)^2\right]\\ &= \frac{E_{\pi_\theta}\left[(\nabla_{\theta_i}\log\pi_{\theta}(X))^2\cdot \left(\log\left(\frac{\pi_\theta(X)}{\pi_{ref}(X)}\right)\right)^2\right]}{E_{\pi_\theta}\left[(\nabla_{\theta_i}\log\pi_{\theta}(X))^2\right]}. \end{align*} $$
然后逐分量使用修正后的估计量,
$$ \nabla_{\theta_i} = \nabla_{\theta_i} \frac{1}{2}(\log\pi_\theta(X) - \log\pi_{ref}(X) - \lambda_i^*)^2. $$
然而这样却很麻烦。首先 $\lambda$ 很难估计,需要先得到score(log prob梯度)才能计算,故可能需要两次backward;其次,每个分量都要单独估计。
作为替代,可考虑使用上一步的score以及单个 $\lambda$ 估计量,
$$ \hat{\lambda}^* = \frac{\sum_i|\nabla_{\theta_{old}}\log\pi_{\theta}(X_i)|_2^2\cdot \left(\log\left(\frac{\pi_\theta(X_i)}{\pi_{ref}(X_i)}\right)\right)^2}{\sum_i|\nabla_{\theta_{old}}\log\pi_{\theta}(X_i)|_2^2}. $$
不过这样仍然较为复杂,需要使用逐样本的grad norm,并且已经引入了一些bias,未必合算。KL loss本身起到的作用也未可知,是否需要在这里做额外的方差减小有待商榷,或许k2即足够。
引用
引用格式如下:
Yang, Xiaobo. (Mar 2025). Gradient Estimation of KL Divergence in Large Language Model Reinforcement Learning. Xiabo’s Blog.
https://xiaobo-yang.github.io/posts/kl_grad/.
或者使用BibTeX格式:
@article{yang2025klgradient,
title = "Gradient Estimation of KL Divergence in Large Language Model Reinforcement Learning.",
author = "Yang, Xiaobo",
journal = "xiaobo-yang.github.io",
year = "2025",
month = "Mar",
url = "https://xiaobo-yang.github.io/posts/kl_grad/"
}
参考
[1] John Schulman “Approximating KL Divergence.” 2020.
[2] Guo et al. “DeepSeek-R1: Incentivizing Reasoning Capability in LLMs via Reinforcement Learning” 2025.